The many “-tance” terms of Electrical Engineering
There are many different types of impedance components and they all rhyme, making it hard to remember which one is which.
Many even have the same units, which can lead to even further confusion.
Don’t let the same “-tance” ending fool you.
If you run into a question on the Electrical PE Exam that asks to solve for one of these components and you aren’t familiar with the exact differences, then you could end up bubbling the wrong answer even if your math and calculations are sound.
Chances are, you’ve already run into a similar mistake or headache while working sample exam practice problems.
To make sure this doesn’t happen on the exam day, let’s take a look at all the different components and define them, as well as understand where each comes from.
First
We’ll start with impedance (Z), a complex number, and take a closer look at both its real and imaginary components resistance (R) and reactance (X).
Second
We’ll deep dive a little further into both types of reactance, inductive reactance (XL) and capacitive reactance (XC).
Third
We will explore admittance (Y), another complex number, and take a closer look at both of its real and imaginary components conductance (G) and susceptance (B).
Impedance (Z)
Impedance is best described as the total opposition of the flow of current through a circuit when voltage is applied. Impedance is a complex number with both a real and imaginary component, it is represented by the capital letter Z, and has the unit of ohms [Ω].
Written in complex rectangular form, impedance looks like this:
Impedance is the sum of resistance (R) and reactance (X).
Resistance is the real component of impedance, or Re{Z} and reactance is the imaginary component of impedance, or Img{Z}.
Impedance is typically represented in a circuit as either a block component:
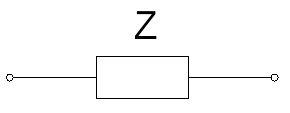
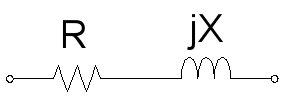
A resistive component with a positive inductive reactance:
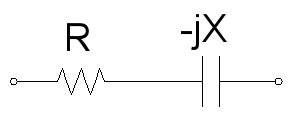
Or a resistive component with a negative capacitive reactance:
Impedance is most often calculated by re-writing ohm’s law to solve for Z:
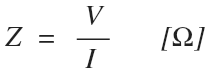
Further recommended reading: https://en.wikipedia.org/wiki/Electrical_impedance
Resistance (R)
Like impedance, resistance also opposes the flow of current when voltage is applied. A purely resistive impedance lacks a reactive impedance component, such as a heating element, radiator, or a resistor.
Resistance is represented by the capital letter R, it is the real component of impedance Re{Z}, and therefore not a complex number, and the unit is ohms [Ω].
A resistance impedance component is represented in a circuit as a resistor:
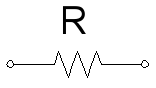
Further recommended reading: https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance
Reactance (X)
There are two types of reactance. Reactance will either oppose the change of current or voltage depending on which of the two types it is.
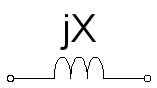
Inductive reactance will oppose the change of current.
Capacitive reactance will oppose the change of voltage.
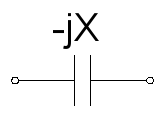
Reactance is represented by the capital letter X, it is the imaginary component of impedance Img{Z}, and therefore not a complex number, and also has the unit of ohms [Ω].
Further recommended reading: https://en.wikipedia.org/wiki/Electrical_reactance
Inductive Reactance (XL) and Inductance (L)
Inductive reactance is one of two types of reactance, and is an imaginary impedance component that opposes the change of current. It is represented by the capital letter X with an L subscript and also has the unit of ohms [Ω].
Inductive reactance in ohms comes from angular frequency in radians per second, times inductance per unit length, times the total length of the component:
Where inductance is measured in total Henrys [H]:
And ω, the angular frequency in radians per second is found by multiplying the 2π times frequency:
In a circuit diagram, inductive reactance is typically represented by a coil, since inductors are typically made by coiling a conductor into the shape of a solenoid.
Inductive reactance will always be a positive imaginary impedance component, or +jX.
inductive reactance resists the flow of current by the magnetic flux that builds around it.
An example of an inductive reactance would be a perfect ideal coil, like the windings in a motor or generator stator.
Further recommended reading: https://en.wikipedia.org/wiki/Inductance
Further recommended reading: https://en.wikipedia.org/wiki/Henry_(unit)
Capacitive Reactance (XC) and Capacitance (C)
Capacitive reactance is one of two types of reactance, and is an imaginary impedance component that opposes the change of voltage. It is represented by the capital letter X with a C subscript and also has the unit of ohms [Ω].
Capacitive reactance in ohms comes from the inverse of the angular frequency in radians per second, times capacitance per unit length, times the total length of the component:
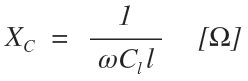
Where capacitance is measured in total Farads [F]:
And ω, the angular frequency in radians per second is found by multiplying the 2π times frequency:
In a circuit diagram, a capacitive reactance is typically represented by the capacitor symbol, since capacitors are typically made up of two conducting plates that are separated by a dielectric medium.
Capacitive reactance resists the flow of voltage by the the buildup of charge between two conducting plates.
Capacitive reactance will always be a negative imaginary impedance component, or -jX.
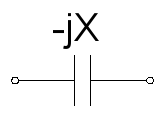
An example of a purely capacitive reactance would be a perfect ideal capacitor.
Further recommended reading: https://en.wikipedia.org/wiki/Capacitance
Further recommended reading: https://en.wikipedia.org/wiki/Farad
Admittance (Y)
Admittance is the opposite of impedance and as such, is best described as how easily current can flow when voltage is applied, or how much current is admitted through the circuit. If impedance is more akin to current friction, then admittance would be comparable to ice or a slippery surface. Admittance is represented by the capital letter Y, and has the unit of Siemens [S], and is a complex number.
Admittance is a complex number because it has both a real and imaginary value.
Written in rectangular form, admittance looks like this:
It is the sum of conductance (G) and susceptance (B).
Conductance is the real component of admittance Re{Y} and susceptance is the imaginary component of admittance Img{Y}.
Admittance is most often calculated by taking the inverse of impedance:
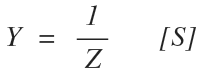
Ohm’s law can also be rewritten to use admittance instead of impedance to solve for both voltage and current:
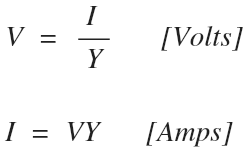
Impedance is often represented using admittance when an impedance component is placed in a circuit such that it creates a shunt (parallel) least resistance path to ground, neutral, or another phase.
Since more current will flow through a path of least resistance (I=V/R), a shunt connection with a very small impedance or large admittance means that the majority of current entering a shared node will flow through it rather than any other path.
Further recommended reading: https://en.wikipedia.org/wiki/Admittance
Conductance (G)
Conductance is the opposite of resistance, it is the real component of admittance Re{Y} and therefore not a complex number, it is represented by the capital letter G, and has the units of Siemens [S]
Conductance is found by taking the inverse of resistance:
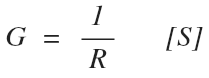
If resistance is the opposition of current, then conductance is how easily current can flow similar to our analogy of ice or a slippery surface compared to friction.
An easy way to remember the definition of conductance is by relating it to how well a circuit will conduct current.
Further recommended reading: https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance
Susceptance (B)
Susceptance is the opposite of reactance, it is the imaginary component of admittance Img{Y} and therefore not a complex number, it is represented by the capital letter B, and has the units of siemens [S]
Susceptance is found by taking the inverse of reactance:
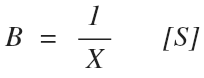
If reactance opposes the change of current or voltage, than susceptance is the quality of how easily current or voltage can change in a circuit.
An easy way to remember the definition of susceptance is by relating it to how susceptible a circuit is to the change of current or voltage.
Further recommended reading: https://en.wikipedia.org/wiki/Susceptance
All recommended reading mentioned in this article
https://en.wikipedia.org/wiki/Electrical_impedance
https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance
https://en.wikipedia.org/wiki/Electrical_reactance
https://en.wikipedia.org/wiki/Inductance
https://en.wikipedia.org/wiki/Henry_(unit)
https://en.wikipedia.org/wiki/Capacitance
https://en.wikipedia.org/wiki/Farad
https://en.wikipedia.org/wiki/Admittance
https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance
Very educative article, detailed explanation and associated illustration…
Makes all the concepts easy to understand. Definitely going into my reference binder!
Great article that discusses the fundamentals of components used in circuit analysis. It’s very easy to forget!
One subject that is covered in this article that is often ignored in most electrical engineering material is admittance. The fact that you tie admittance, conductance, and susceptance back to impedance, resistance, and reactance is a tremendous help with learning these terms and concepts.
Thanks Michael, glad you enjoyed the article.
Zach,
Great summary of all these terms. Not only you break down the concepts behind these terms, but also provide a way to remember them. Finally, someone helped me make sense of all these and helped me commit to my memory.
Hello Zach,
In the Admittance (Y) part , you used some ” Impedance” words that I believed that supposed to be ” Admittance”. Would you please read through the Admittance (Y) section and fix it? Other than that, I am very satisfy with your explanation.
Hi Trung,
Thanks for your comment.
I read through the Admittance (Y) section but did not identify any missuse of the word “impedance.” There are several points in the section where admittance is compared and contrasted to impedance to help explain the concept of admittance.
If there are any particular points of the article or Admittance (Y) section that you are unsure of feel free to reply and I will do my best to clarify.
Thanks!
Zach,
I believe he is referring to the Admittance section where it states: “Impedance is most often calculated by taking the inverse of impedance.”
I believe it should say Admittance is the inverse of Impedance as specified in the equation that follows.
Thanks for helping me spot it David! I’ve since updated the article to read “Admittance is most often calculated by taking the inverse of impedance” instead.
Zach, good general information to brush up on. Clears up any doubt for easy lookup
I was a bit confused after reading/listening to the course but this really helped clear things up, (the fact that you emphasize the difference during each live class is also very helpful).
Hello Zach,
Is the formula for inductance X_l=w*L or X_l=w*L*l (similar question for capacitance)? I haven’t seen or noticed “total length of the competent” in previous equations.
Thank You,
Hi Ahmed,
Inductance (L) is in the unit of henries (H).
Inductive reactance (X or X_L) is in the unit of omhs (Ω).
The formula you wrote above is for inductive reactance (X or X_L) and not Inductance (L).
The formula for inductive reactance (X or X_L) will include length (l) anytime the inductance (L) is given in per unit length.
For example, if the inductance is L = 0.001 Henries per 1,000 ft, then you’ll need to multiply by the total length of feet in the formula. For example, suppose there is 100 feet of the above inductance:
X_L = wLl
X_L = (2π60)(0.001 H/1,000ft)(100 ft)
X_L = 0.038Ω
I was reading the document and I think you have a typo. In the Admittance section, it says
“Impedance is a complex number because it has both a real and imaginary value.
Written in rectangular form, admittance looks like this:
admittance is the sum of conductance and susceptance”
Shouldn’t it say instead,
Admittance is a complex number because it has both a real and imaginary value?
Hi Jacob,
You are correct. Like impedance (Z), admittance (Y) is also a complex number.
Just as impedance is the sum of resistance and reactance, admittance is the sum of conductance and susceptance.
These are the real and imaginary components of each complex number.
Great summary of the dreaded -ances. I see the typo Jacob was referring to. It’s in the second paragraph under the Admittance section.
“…Admittance is represented by the capital letter Y, and has the unit of Siemens [S], and is a complex number.
Impedance is a complex number because it has both a real and imaginary value.
Written in rectangular form, admittance looks like this…”
In the second sentence quoted above, you accidentally plugged in “impedance” instead of “admittance”. You already explained that impedance was complex in an earlier section. Here is where you meant you say admittance was complex as well.
And a little bit later in that same section, there’s this sentence:
“Impedance is most often represented by its admittance ***antinome*** when an impedance component is placed in a circuit such that it creates a shunt (parallel) least resistance path to ground, neutral, or another phase.”
And I’m pretty sure you meant “anytime” instead of “antinome” in that sentence. 🙂
Thanks Josh! I see it now