I want to share with you the the most common mistakes that students make with three phase power formulas that lead them to getting robbed of correct answers on the PE exam, and remind you why specific notation is so important.
My goal of this article is to get you out of the bad habit of not using proper notation when you write down formulas and to help you avoid the biggest pitfalls to applying apparent power and complex formulas correctly.
You know the drill.
You get to an easy question and you smile to yourself with relief on the inside. It’s a type of question you’ve answered countless times before and always get it right, and there are not too many steps involved in solving it.
So you write down the formula, punch in a few numbers in your calculator, and circle the right answer.
You check the answer with the solution right before moving on to the next question and to your surprise – it’s wrong.
Sound familiar?
There are a few specific topics on the electrical power PE exam that this is most likely to happen, and one of them is three phase power.
What we want to know is:
- Why does this happen?
- How can we prevent this from happening again? (Especially on the exam).
Most of us, are very familiar with using and writing down the following three phase power formula like this, without taking care to use proper notation:
![]()
Let’s see what happens when we use this formula under the stress of exam conditions.
A three phase power question appears:
“A three phase wye connected load draws a current of 150A<-25° Amps with an applied line to neutral voltage of 277 volts. Find the total complex power”
You start to solve it using the trusted three phase apparent power formula shown above:
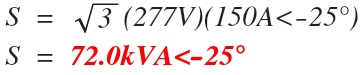
If you make this mistake then you end up with the wrong answer.
The two biggest mistakes I see made over and over by students with apparent power is:
- Misusing the three phase power formula that uses the square root of three and line values to accidentally solve for complex power instead of magnitude
- Forgetting to use the current conjugate when solving for complex power
Let’s take a look at both, and see how they apply to the above example so that you don’t make the same mistake on the PE exam.
Mistake #1 – Misusing the three phase power formula that uses the square root of three and line values to accidentally solve for complex power instead of magnitude
The correct way to write the three phase apparent power formula that uses the square root of three is not like this (incorrect):
Instead, get used to writing it down with the proper notation that will save you in the future (correct):
![]()
I know what you are thinking. The differences are so minor, does it really matter? Well the devil is in the details and it’s these small details that can prevent you from making costly mistakes and that risk a failing score.
First thing – This formula should only be used for magnitude. That means the VA value of S without the phase angle.
If you were to draw a power triangle it would be the length of the hypotenuse only without direction (angle).
The brackets around S tell you that this equation is only going to solve for magnitude, and the three phase subscript (3φ) reminds you that you are working with a three phase quantity so that you don’t attempt to convert to a three phase quantity by accident.
![]()
Next, the brackets around V and I tell you that you are only to use the magnitudes of both voltage and current in this formula, and the line subscript (L) tells you that you are only to use line values for both:
![]()
Let’s use the formula to solve for the correct magnitude of three phase complex power:
“A three phase wye connected load draws a current of 150A<-25° Amps with an applied line to neutral voltage of 277 volts. Find the total apparent power”

The apparent power (magnitude only) is equal to 124.7kVA.
That’s it. No angle.
(note that I did convert the phase voltage magnitude given in the problem to line voltage magnitude first using √3(277V)=479.8V)
Try to burn it into your head as soon as possible that this formula is used for magnitude and magnitude only, not complex power.
Mistake #2 – Forgetting to use the current conjugate when solving for complex power
The example question asks for complex apparent power, which includes magnitude and angle, or real plus imaginary components.
Using the above formula with the square root of three and line values only gives us magnitude.
The most appropriate formula to use to answer this question would be (correct):
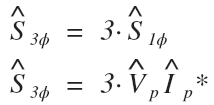
Which brings us to the second biggest mistake students make when using apparent power formulas: forgetting to use the current conjugate.
Most of us in our mind, know that power is “equal to the voltage times current”.
The result of this is getting into the bad habit of writing it down like this (incorrect):
![]()
Notice the lack of notation:
You should get into the habit early of asking yourself:
Are these complex numbers (vectors)?
Should there be a conjugate in my formula?
Are these magnitudes?
Are these phase values?
Are these line values?
Even if we remember to multiply the results by 3 to get three phase apparent power, we are still likely to get it wrong because of the missing notation in the formula that helps to prevent us from making costly mistakes by guiding us to use the correct values and correct formulas for the value we are solving for.
Proper notation is extremely helpful, get into the habit of using it early on if you want to dramatically improve your score on the PE exam by reducing costly mistakes.
Let’s take a look at the correct formula again and break down each specific notation piece by piece and see why each one is important:
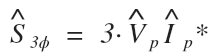
First off the lack of magnitude brackets and the included “vector hat” let us know we are solving for complex power. This means our answer will have both magnitude and angle.
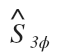
This tells us the answer will be in the form of a complex value either in polar or rectangular form, not just the magnitude:
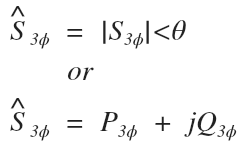
Next, the ” vector hats” above both V and I also tell us we are using the complex values of both voltage and current, and the phase subscript (p) tells us that if we want to get the correct answer, we need to use the phase values for both voltage and current:
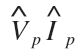
And last, the conjugate symbol (*) after the phase current Ip tells us that the polarity of the phase current angle must be changed so that it gets subtracted from the voltage phase angle instead of adding to it.
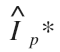
In other words, if the phase current has a positive angle, you must change it to negative; and if it has a negative angle, you must change it to positive.
Let’s look at how the conjugate is applied, and then we will solve the example question for the correct answer by using this formula.
Pay attention to the conjugate in red:
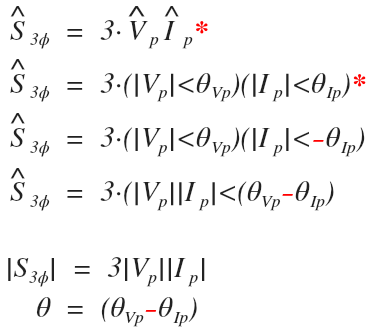
Notice how even though we just solved for three phase apparent power, the angle is the difference of the single phase values and NOT the three phase values.
This is why the magnitude and the phase angle were incorrect in the first example.
Had enough yet?
Let’s wrap this up and solve the original question using the formulas correctly:
“A three phase wye connected load draws a current of 150A<-25° Amps with an applied line to neutral voltage of 277 volts. Find the total complex power”
Pay attention to the correct use of the conjugate in red and how it changes the polarity of the current angle:

Let’s compare this to the answers we got with the other examples in this article:
“A three phase wye connected load draws a current of 150A<-25° Amps with an applied line to neutral voltage of 277 volts. Find the total complex power”
Incorrect:
![]()
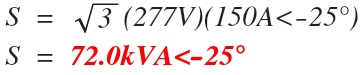
Correct for apparent power (the magnitude of complex power):

Correct for complex power (magnitude AND angle):

If you enjoyed this article, the Power Fundamentals Boot Camp goes into much more detail for all power formulas:
Electrical PE Review – Power Fundamentals
Thoughts? Want to share? Still confused?
Comment below to add to the discussion or ask a question. I try to respond within 24 hours or sooner.

Awesome! As usual, thanks!
Glad it helps. Don’t forget to print it out and add it to your three ring binder of references to take with you to the exam.
Zach Stone, P.E.
Zach, this was very helpful.
However one question?:
Why when working some problems, in the solution, I see PF show up at times and other times not?
Exp: calculate three phase power or line current for a system.
I would use the formula below;
S = (Sqr rt 3)(V) x (I conjugate) x(PF)
Should you always include power factor if you have it or if it is given?
Jeff,
Can you site the specific example, is it from my course or another resource?
Be careful, the formula you used is not correct, take a look:
“Exp: calculate three phase power or line current for a system.
I would use the formula below;
S = (Sqr rt 3)(V) x (I conjugate) x(PF)”
Multiplying by PF will give you active power in watts (P), not apparent power in VA (S). You have the above formula set equal to apparent power (S) on the left, but the math on the right side of the equation will calculate active power (P).
Remember that power factor is also the ratio of active power in Watts to apparent power in Volt-Amps, or: PF = P/|S| = (Watts/VA) = Cos(θ)
If the problem asks for Power but does not specify Apparent/Complex (S in VA) or Real/Active (P in Watts) then look at the answers.
Are they in watts?
Then solve for P:
P = |S|·PF = |Vp|·|Ip|·PF (For single Phase)
P = |S|·PF = √3·|VL|·|IL|·PF (For three phase)
Or are they in Volt-Amps (VA)?
Then solve for S:
S=Vp·Ip* (for single phase magnitude and angle)
|S|=|Vp|·|Ip| (for single phase magnitude only)
S=3·Vp·Ip* (for three phase magnitude and angle)
|S|=3·|Vp|·|Ip| (for three phase magnitude only)
|S|=√3·|VL|·|IL| (for three phase magnitude only)
The current conjugate is only used when finding total complex apparent power in Volt Amps *with the apparent power angle*.
If you are only finding the magnitude of apparent power, i.e. the problem asks to find apparent power and there are no angles in the answers, only VA values, then don’t worry about using the conjugate or phase angles for voltage and current, just multiplier their magnitudes together.
Make sense?
Zach Stone, P.E.
Zach,
Your response brought me so much clarity!! This summarizes it all. Thank you!!
Just a quick correction Zack PF = Real Power / Apparent Power or PF = Watts/VA not VA/Watts!
Good eye Memon, thanks for catching that mistake! I’ve got ahead and corrected the comment so that it is correct.
Zach, you are the GOAT! Thanks for making this available for free. This really cleared up any confusion I had lingering.
Thanks Mortimer! Glad that an article I wrote back in 2017 is still finding other engineers and helping them!
This was a great run through of common mistakes made. I especially will take note to be more diligent with the added symbols and subscripts to ensure a full understanding of the formulas.
I’ll admit that these mistakes have tricked me in the past.
Thank you for the article, also the video on the subject was very informative as well.
This article helped me to get a clear idea about S=VI*, which helps me to solve the problems without any confusion.
I have already printed this set of rules in my reference binder for the exam. I’ve referenced it a number of times even in working Zach’s problems in the Review Course. Working thru it has helped me commit to memory what are appropriate ways to work with 3 phase power and what aren’t.
This article cleared the most obstacles I had in applying apparent power formulas. It was helpful indeed.
Always! forget to change the angle of current
Now I think I won’t do this mistake again
Just remember S=VI*
Thanks Zach ….
I agree that this is a simple formula that can be misapplied so many times. There have been a lot of times I have forgotten to multiply the conjugate of the current while I was trying to calculate the apparent power. Thank you for the simple clarification. This explanation needs to be on the front of everyone’s cheat sheet.
So true about this formula, Im certain ive made the same mistakes, especially the conjugate mistake. I will be making a stronger effort to write out all the notation.
Thanks Zach! Very helpful. This article makes it so clear when to use the Line vs phase values as well as the differences between when finding Magnitude only vs complex power which is magnitude and direction. I loved how clear it makes when and how to apply conjugate!
Great article! This article is a succinct explanation of knowing when and how to apply each formula in order to make sure that you don’t get tripped up when trying to solve for what the question is asking for, whether it be a magnitude or a complex vaule.
Zach,
after your email mandating me to read this (you said it in a nice way), it puts into context how to apply these formulas. This is the second time I’ve read through this, but it took actually missing some problems to see the errors. Good article.
Hahaha, like good medicine it may not taste the best but we’re glad we put it down. Glad it helped.
The Biggest suggestion I can offer is to get in the habit of writing proper notation with vector hats for complex phasor values and brackets for magnitudes. This will help make sure you use the proper formulas and it will beat into your mind the subtle differences that result in getting the correct or incorrect answer.
I’m guilty of this. I get in such a rush working out problems that I forget to put vector hats and magnitudes on my problems. Even though it’s a timed test, it doesn’t take that long to show the details on the problem to ensure I have the right formula for the solution.
This was an excellent article making the misconceptions crystal clear. It gets confusing between 1 phase and 3 phase formulas but techniques taught by Zach will remain with me forever now. Thank you.
Extremely helpful! The way that you break down the explanation of when to use root 3 and when to just multiply by 3 is awesome! I’ve taken other courses and the course instructors could not even get these formulas right! You have definitely simplified 3 phase power!
Great article. It’s a great reminder to take your time and not make any silly mistakes.
Thank you for the article, also the video on the subject was very informative as well.
this was extremely helpful . must must must have knowledge for exam . the best part is you laid it out in there in the best short simple and straight forward manner. simple explanation makes understanding better. Not to forget that i admit that these mistakes have tricked me in the past.
thanks a lot Zach, the different I notice about you and your classes, you really can tell that you care, you are one step ahead and prepared for even the misunderstanding and common tricks, and you are very honest to avoid any chances of mistakes and repeat may times to get us to get to understand and never memorize. I learned a lot from you, thanks
I guarantee you that Zach’s PE power equation cheat sheet and insistence that the students draw phasor diagrams for each problem, use units and carefully apply the 1- and 3-phase apparent power equations will save your bacon when the test rolls around. I have caught myself trying to rush and missing an answer on the sample tests (NCEES, Complex Imaginary, A.S.Graffeo) because I didn’t draw the situation. As he showed in one of our live classes, it only takes a short period of time to graphically represent the situation actually SEE the answer the questions asks. I found I had to unlearn the bad/lazy habits I picked up when referencing power in my daily work. I am glad I started about 3 months before the exam and now I can tell which equation and which PF angle to use every time!
Doing Zach’s would have been worth it just for the material on three phase power relationships. It’s something I learned well enough in school to pass tests, but never fully grasped. I now feel like I have a much deeper understanding on this area, and this article is definitely a great reference to refresh my memory before the test.
Thanks Seth! Glad you enjoyed the emphasis on three phase power relationships. It tends to be one of the more common areas where avoidable mistakes get made that can cost points on the exam.
I have no more confusion using power formula after reading this article. Thanks Zach!
I made the same mistakes. Truly a great article on how to solve complex power. This helped me solve the most complicated power system to an equivalent circuit and back to three phase. Thank you Zach for show us the way. You truly made me have a better understanding of electrical engineering.
Thanks for the kind words Carlos!
A must printout article for the PE Exam. I still use it as reference to check my work. i recommend to practice solving complex problems and magnitude only based on what you already know and you’ll be surprised at the small and important steps you miss. Now start using this article as reference and you’ll learn to appreciate Zach’s explanation and simple steps to follow to get the correct answer. A very essential and important article to read and printout for the PE Exam to use as reference and check your work.
So good to have these three-phase power problems on a single page. Very helpful to get over the common mistakes- which I tend to fall for quite often. Hopefully I will get over with them now. Thank you.
I like the comparison chart. I am guilty of tripping over these mistakes or forgetting the phase shifts when converting. Definitely a habit that needs to be corrected.
As usual, this is an in depth explanation that has simplified an otherwise confusing topic. Thank you, Zach!
Probably still the best game-changing tip. This is forever engrained in my head. Thanks Zach!
have made these mistakes before. I feel that this article has helped me improve in making these mistakes less. Great read to try to avoid these mistakes.
Amazing way of teaching technical material! Thanks Zach. This article really helped me to find out where were my mistakes and how to address them. This is a very tricky subject which spreads out, almost, all over the PE exam. Thank you.
Thank you for calling out the common “minefield” of power problems. This article help clarify the when to use phase voltage or line voltage in solving power problems.
I’ve printed this article out as a reference and came back to it multiple times in my studies. Thank you Zach for helping me not get tripped up on questions using complex power.
Great reference article to take with me to the PE exam. Surely helps avoid simple mistakes.
The only thing that gets me here is knowing when to omit the sqrt(3) for certain cases in per-unit where it is already included in the base values.
Zac, you should open power engineering school, I wish i had a professor like you in college.
Hi Zach,
You explained these most common errors so well, that maybe you are able to help me also with the following question.
In textbooks, you can often find the following formula for three-phase apparent power:
S=sqrt(3)·U·I*
(all variables are vectors, although I’m unable to write them as such in this simple text editor)
This should be the same as
S=3·Up·I*
…but they are not. The line-to-line voltage U has different angle than the phase-to-neutral voltage Up. In order to get the same results with these formulas, you have to assume that the U has the same angle as Up, although in reality the angle of U is 30 degrees larger than the angle of Up.
Why the aforementioned formula is used in textbooks if it’s “clearly” erroneus. Is there perhaps some kind of logic to this formula that I just don’t understand?
In the many power books and white papers that I have read, I’ve seen that formula used in the complex vector form only once and it was accompanied with a lagging 30-degree phase shift to account for using the complex line voltage in order to still get the correct power angle.
Typically, that formula is used as the three-phase apparent power formula with magnitudes only as discussed in this article in which case the power angle is typically derived from the power factor which is usually given.
If you have specific examples in books or white papers where you have seen that formula used in complex vector form I’d be happy to take a look.
The NCEES PE Hanbook has the formula S = 3*Vp*Ip = Root(3)*V-L*I-L(Cosϴp – jSinϴp)
I am confused why they use they use the phase angle difference between the phase voltage and phase current when using line quantities.
Hi Robert,
Good eye. I will agree that it is a very odd way to represent three-phase complex power in rectangular form.
I’m not sure which book NCEES® borrowed this particular version of the formula when putting together the Reference Handbook, but I would not use it.
Essentially, this version of the formula separates the magnitude of complex power (√3·V_L·I_L) from the real and imaginary components (Cosϴp, and jSinϴpp).
To avoid confusion and making mistakes, I strongly recommend using the complex power formulas we teach during our live class semester that can also be found in the boot camps.
Zach,
In both scenarios above, the questions asked to Find the (total complex power) both times. How I know the first one is asking for magnitude only and second time for magnitude and phase angel ??
Hi Zach,
Thank you for this thorough and well described guide. Its may be a silly question but if you can clear my confusion.
I’m working with a three phase meter having three different current phase angles (60 , 120, 225). I want to calculate Active Power. how I’m going to calculate PF with these angles.
Meter is running on 120 volts and 50Amps per phase. Voltage angles are 120.
Any help in this regard will be highly appreciated.
Should you add that “Line current is equal to phase current for Wye connected system”? It was implied but not mentioned in the above explanation.