Have you ever noticed that the fraction in the formula for base changing per unit (or percent) impedance appears to be upsidedown?

For example, when compared to the standard per-unit base change formula shown below, the new base and the old base appear to have switched places:
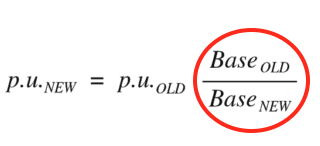
In this article, I’m going to show you that surprisingly, both formulas are actually identical. Click play on the first video below to begin.
Part 1 of 2 – Deriving the Per Unit Impedance and Percent Impedance Base Change Formulas
*Related Content – Are you new to the per unit system or not familiar with dividing a one line diagram into different “voltage zones” created by each transformer? It may be helpful to work your way through our worked out example on the per unit system prior to diving into the base changing formulas discussed below: Per Unit Example – How To, Tips, Tricks, and What to Watch Out for on the Electrical Pe Exam.
Regardless of how far along you are in studying for the electrical PE exam, chances are you are already familiar with expressing a value in the per unit system by dividing the value by its base value:

For example: 150 amps expressed in the per unit system with a base value of 200 amps is a per unit current of 0.75:
Ipu = I/Ib
Ipu = 150A/200A
Ipu = 0.75
Similarly, it’s not too much work to base change a per unit value to a new base by multiplying the old per unit value by the old base, then dividing by the new base:
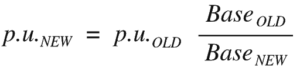
For example: the same 0.75 pu of current expressed in the previous base of 200 amps will be equal to 0.6 pu when expressed in a new base of 250 amps:
Ipu new = Ipu old (Ib old/Ib new)
Ipu new =0.75(200A/250A)
Ipu new = 0.6 pu
What happens when we try to apply this same method of base changing to per unit impedance values and percent impedance values?
Have you ever noticed that the formulas used in reference books and most practice exams for base changing per unit impedance and percent impedance values seem to have the old base and new base on the wrong side of the faction?
For example, the most common per unit impedance and percent impedance base change formula you typically see is the old per unit impedance (or old percent impedance) multiplied by the new power base then divided by the old power base:

Why does the per unit impedance and percent impedance base change formula have the new power base on the top of the fraction and the old power base on the bottom of the fraction instead?
The other formula for per unit impedance and percent impedance base changing you may have come across in a reference book or practice exam has the square of the old voltage base to the new voltage base ratio like this:

Where does this formula come from?
In the Part 1 video of base changing per unit impedance embedded at the top of this article, we answer each of these questions and show how all three of these formulas are actually the same during the special condition which exists when the old and new voltage bases are equal, even though the old and new power base values in the formula seem to be in the wrong places. We also show where the formula with the square of the old voltage base to the new voltage base ratio comes from.
Part 2 of 2 – A Worked Out Example Practice Problem of Base Changing a Generator Percent Impedance
In the Part 2 video of base changing per unit impedance embedded directly above, we go over a worked-out example of base changing the 5.9% impedance of the generator in the one-line diagram shown below using the ratings of transformer T2 as the new system base values:
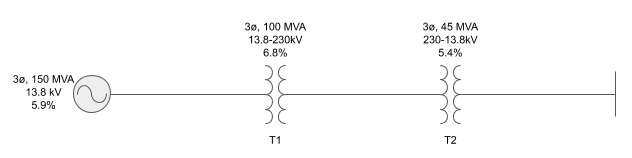
We base change the generator percent impedance using the longer worked out per unit base change formula in order to show that since the old and new voltage bases are equal, the voltage terms in the base change formula cancel, leaving us with the “short cut” percent impedance base change formula that requires the power bases.
We also show how to recognize when the old and new voltage bases are equal, so that you know when it is safe to use the shortened base change formula in order to stay out of trouble or to prevent you from attempting to use this formula when this is not the case.
Remember, you can only use the shortened formula when the old and new voltage bases are equal. If they are not equal, you’ll have to use the longer form of the formula in order to get an accurate answer.
*Related Content – Are you new to the per unit system or not familiar with dividing a one line diagram into different “voltage zones” created by each transformer? I recommend grabbing a pencil and paper and working your way through our worked out example on the per unit system: Per Unit Example – How To, Tips, Tricks, and What to Watch Out for on the Electrical Pe Exam.

Printed this off and put in my binder, will be sure to reference during the exam to clear up any confusion with all per unit problems.
Thanks!
Glad you found it helpful.
great thanks
it is very useful
Hi Zach, I understand how you got the formulas, but old/new will give you a different answer from new/old. Does new/old only work when dealing with apparent power?
Hi Eric,
“Does new/old only work when dealing with apparent power?”
The key to remember is that we are not base changing an apparent power value, we are base changing an impedance value. The old and new voltage base must be equal so that they cancel when they are plugged into the impedance base change formula.
Try working along with the example that is demonstrated in the second video of this article for an example of this.
Hi Zach, thank you for this video. Can we use the formula below to derive new Zpu if old and new voltage and apparent values are different?
Zpu-new = Zpu-oldx(SB-New/SB-Old)x(VB-Old/VB-New)^2
Absolutely Sridhar, just like we used that formula in the second video of this article in the worked out practice problem.
Can you work out this example choosing the rating of transformer T1 as the power base.
Hi Sadrac, if you’d like to attempt this on your own and post your work showing all of the steps in the comment section I’d be happy to take a look and check your work.
I did the problem using T1 as my base value and everything was still the same except for my Sb=100MVA so my Zpu-new= 5.9% X (100MVA/150MVA) = 0.0393= 3.93%
Hi Cynthia and Sadrac,
I’m also attempting the problem you posted, using T1 as the new base. I’m getting the following:
Zpu-new= 5.9% X (100MVA/150MVA) X (13.8kV/230kV)^2 = 0.0001416
I believe Cynthia’s approach is incorrect since the final voltage is different, since we’re looking at T1 instead of T2. Let me know of any thoughts.
Figure Q2 shows a single line diagram (SLD) for an 11 kV interconnected network. The 33/11 kV transformers at each substation are shown along with the connector between the 11kV bus-bars. Based on the normally open point being closed and a fault at the 11kV busbar at substation B:
a) Select an appropriate power base and calculate all of the reactances in pu form.
b) Sketch a single line reactance diagram, including component values, to represent Figure Q4.
c) Apply circuit reduction techniques to reduce the equivalent circuit in (b) to a single impedance.
d) Calculate the fault level and fault current.
can you help to solve this
Hi Zach,
For a line impedance at the secondary side of the transformer to be converted to a common base impedance at the primary, is the formula below right?
Z new pu = [(kV pri ^2) / (kV sec ^2) ] * Z line / Z base
Thank you
Hi Chris,
If the line impedance is expressed in ohms [Ω] and not per unit [pu], then all you need to do is divide the impedance of the line in ohms [Z] by the new base impedance [ZB] of the voltage zone the impedance is located in.
For a quick example, take a look at the following article on the per-unit system:
https://www.electricalpereview.com/per-unit-example-tips-tricks-watch-electrical-pe-exam/#comment-2776
Particularly step #4 for the 5 + j15Ω line impedance located in Zone 2 the 200Ω load located in Zone 3.
If by comparison the line impedance is already expressed in per unit [pu] instead of ohms [Ω], then chances are you won’t really need to base change it since unlike a transformer or generator, the only time a line impedance is expressed in per unit is when the entire system has already been converted to a common base.
If for some reason you are asked to base change a line impedance already expressed in per unit [pu] to a new base, then you would follow the same steps as base changing any per unit impedance as described in this article or the steps in the article link in my comment above.
Thanks!