Related Article:
Try our fully worked out Per Unit Example with the following free article:
Electrical PE Review – Per Unit Example: Tips, Tricks, and What to Watch Out for
Imagine you come across a three phase system with per unit impedances and you need to calculate the actual value in ohms:
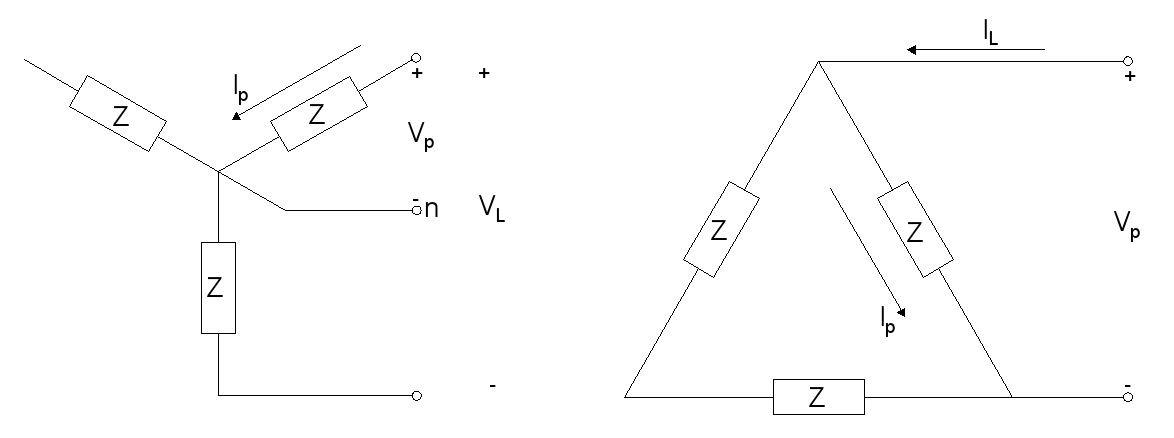
No sweat, right?
You know that actual values are simply found by multiplying per unit values by their base values.
So you start to calculate the base impedance value by writing down power formulas and ohms law but then remember we are dealing with a three phase system. You come to following mental cross road.
Do we:
- Use phase voltage?
- Line voltage?
- Single phase power?
- Three phase power?
- …What about the square root of three?
I bet everyone reading this has run into this situation at some point or another.
When you are calculating impedance (or base impedance), you can actually use single phase or three phase values like this:
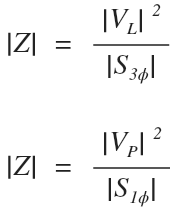
Both formulas will result with the correct value in ohms.
So the question is – how is that possible and where did the square root of three go?
Let’s take a look and see how we can derive the solution.
We’ll start with a single phase circuit and work only with magnitudes for the sake of simplicity. On the PE exam or a practice problem, you will most likely need to work with complex values (both magnitude AND angle).
For extra practice, I encourage you to try repeating this exercise on your own using the complex polar values for each variable, being extra careful with the current conjugate.
Ready? Here is our single phase diagram:
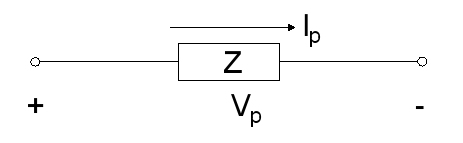
To start, let’s solve Ohm’s law for current (I), substitute it into the single phase apparent power formula (II), and then solve for impedance (III):
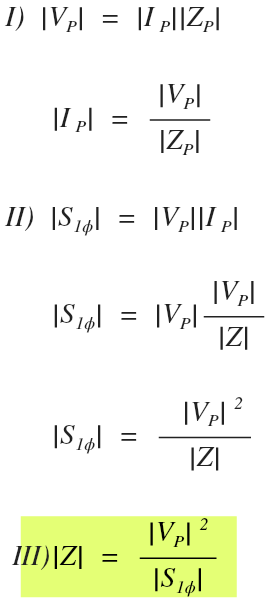
That explains how we solve for impedance using single phase values in a single phase circuit.
Now let’s take that same equation and substitute three phase values and see what happens.
We’ll start with the formula that calculates the magnitude of phase voltage from line voltage (I), followed by the formula that calculates single phase apparent power from three phase apparent power (II), then we will substitute both formulas into the impedance formula we arrived at above (III):
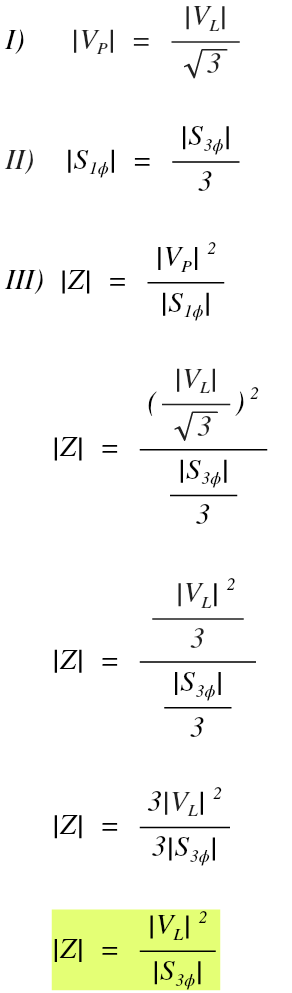
The square root of three on the top of the fraction gets canceled out with the three on the bottom of the fraction after being squared.
This means that to find impedance for a three phase circuit, we can use line voltage and three phase apparent power, OR, we can use phase voltage and single phase power. Both will result in the same value in ohms for impedance:
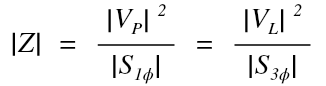
And the last step, if we want to find base impedance, all we have to do is use the base values for both voltage and apparent power:
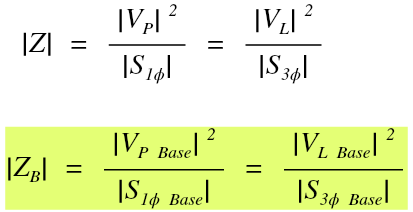
And of course, this applies to a load whether it is wye or delta connected:

Want more practice with the Per Unit System?
Try our fully worked out Per Unit Example with the following free article:
Electrical PE Review – Per Unit Example: Tips, Tricks, and What to Watch Out for
Make sense?
Learning how to derive relationships with different formulas like we just did above is a powerful skill. Once you get comfortable doing it, you will be able to answer many uncertainties you have by being able to prove or disprove certain relationships.
Leave your questions below that you’d like answered or share your experiences.

This was a great article to read. It was good to see how to derive certain formulas explaining how I have it on my “cheat sheets”. I’ll admit the 3 phase and phase and line voltages can get very confusing but this article and other videos have explained it clearly and simply to make it much easier to understand. Thanks!
Great Feedback Earl I’m glad it was helpful!
One of the biggest issues I ran into when I took the exam many years ago was confusing single phase and three phase formulas and values but it’s pretty easy to get right every time once you peak behind the curtain and dig deeper into the math.
What about solving for base impedance by first solving for base current with a 3 phase transformer? Currently, any problem I’ve come across that first solves for base current and then base impedance with a 3 phase transformer does not equal the base impedance found by using equation V-L/S.
Hi Steve,
You would still solve for the base impedance using the above formulas using the selected bases values for V and S. If you’ve selected a transformer’s rated values as base, then you would use the S and V rating of the transformer. The value for base impedance will be different across a transformer where there are more than one “voltage zones.” For more information please see the following Per Unit Article:
electricalpereview.com/per-unit-example-tips-tricks-watch-electrical-pe-exam/
This article helped me to get a clear idea about single phase and three phase formulas and I was always confused with square root 3, this article really helped me.
This worth being in the first page of my cheat sheet. Thanks Zach’s.
Well organized explanation, I have printed and added to my 3 ring binder, thanks Zach …
So great, I have so much trouble with per unit problems. I get so confused with this topic and this will help. This is also going into my cheat sheet book.
Is there a good way to print these articles while not printing the comment section, or the header?
This is the best article to read and learn the difference between phase current and line current values for delta system. Thanks Zach.
I have seen in the books that they solved for Z using matrix forms in the transformer connections. Can we apply the matrix forms to solve for Z for load connections and how?
Typically you are only going to see that for unbalanced systems. Unless you are working in the protection industry it is not really required, and even then everything is done by software now. Almost all problems on the PE exam will be balanced systems, the few that are not the problem will specify and give you enough information that maxtrix operation (linear algebra) is not necessary.
This article clarified a lot. I just printed this article. Thanks Zach!
Clear and concise. Best part for me is the statement : “And of course, this applies to a load whether it is wye or delta connected”. Thanks Zach!
This article explains well how both the single phase and three phase values for voltage and current can be used when determining base values for impedance, removing some of the uncertainty associated with it.
Couldn’t be simpler than that to understand, Thank you Zach.
Thanks Anmar! You are most welcome.
Great article. This helps on explaining why we don’t need the square root of 3 in per unit whether we have a 3-phase or 1-phase system. Thanks Zach!
My review of the sample PE exams concluded that knowledge of when to use single- or three-phase values would affect every section of the exam. The explanations offered by Zach will provide a rock solid foundation and an excellent reference for most of the circuit analysis problems. I appreciate that he spends enough time on the topic to make sure we can speak the “test” language without overloading the theory. As he mentions often, “the test is a mile wide and an inch deep.” . His explanations keep us focused on the important topics at the appropriate depth.
Thanks for the kind words Damian!
Very helpful. It clears my confusion about impedance formula.
Thank you very much. With a simple explanation, I understand this very easily. Great !!
Glad it helped!
Great Review,
I am just a little confused. The three phase apparent power equation is S3p=Root3*Vline*Iline * when you solve for three phase apparent power from your above equation I get S3p=Vline^2/Z there is no root three in the equation.
Thank you
Think of a delta 3 ph ckt
S3p = root3*VL*IL
= root3*VL*(root3*Iph)
(since IL=root3*Iph
= root3*VL*(root3*Vph/Z)
= 3*VL*VL/Z
=3*VL^2/Z
Think of a star connected 3 ph ckt
S3p = root3*VL*IL
= root3*lL*(root3*Vph)
= root3*VL*(root3*Vph/Z)
= 3*VL*VL/Z
(since VL=root3*Vph
=3*VL^2/Z
Now ask jach to clarify the presence of 3 not appearing in his formula
This calculation is only true for star connected 3 phase system.
For delta connnection you have Vph =VL
So Z= Vph^2/S1ph=VL^2/(S3ph/3) =3VL^2/S3ph
So you will land up to a different value. Isn’t it
Yes sir but wye and delta connections tha give valu is line volatage or phase voltage clear it
Great article Zach. How about the other electrical quantities such as Current, Voltage and Power? You explained that Impedance can be calculated using either 3 phase power and line to line quantities or single phase quantities, they yield the same result.
Can you apply the same concept to other electrical quantities? such as when finding per unit current, per unit voltage, per unit power. There are 4 main electrical quantities and this article talks about impedance.
Hi Mark, thanks for your comment. There is a wealth of more information available in the other free articles on our website, similar to this one. For more examples of the per unit system I suggest this article: https://www.electricalpereview.com/per-unit-example-tips-tricks-watch-electrical-pe-exam/ There is also additional free content on our YouTube channel: https://www.youtube.com/channel/UCy5dChpJOpYMdc-7JJff-qg and in our online review course.
Hi Zach,
Let’s says the electrical system is comprised of Generator(200 MVA, 13.8KV), transformer(300 MVA, 13.8/480), transmission line & load etc; You are asked to draw a reactance diagram in PU. I understand how to compute per unit reactance. When you draw a reactance diagram your generator, transformer, loads are 3 phase values, you don’t convert them into per phase except the transmission line impedance is per phase. I thought you would take everything on per phase basis? This is really confusing me. I have watched several of your videos. I know how to convert and stuff, just don’t know what should be used in per phase and what should be used in 3 phase. May be I am making this way more complicated that it really is. Can you please straighten my thinking?
Hi Roy, thanks for your comment. Just like the comment above you I suggest working out our detailed per unit example in the following article: https://www.electricalpereview.com/per-unit-example-tips-tricks-watch-electrical-pe-exam/ I think it will help clear things up for you and provide more practice.
I want know the difference between Zbase in star and Zbase in delta?
Hi Sundara,
This doesn’t really make a difference since base impedance is a calculated value derived from the chosen base voltage and base power in the form of Z_Base = V_Base^2/S_Base
Great article Zach. It really helped to consider all the details when solving the problems which require all the P.U quantities, especially when solving for fault current and not sure if we should use 3phase values or single phase! Thank you.
This works out on paper but always good to have that better understanding. Thanks
Zach, this is extremely helpful since p.u. wasn’t something I was exposed to in college, great explanation for reference.
I’ve never been able to wrap my head around per unit equations until I read this article and took Zach’s class for the PE Exam! This is great stuff!
To shed some light on your beautiful formula, no it does not work for delta connected Generators, because line and phase voltages are same so the √3 is not cancelled from the numerator and only 1 phase formula is applicable for delta.
Nice ! Fantastic. Thank you
Very good explanation helped a lot
How to measure impedance for three phase delta motor; current is measured on all three conductors; voltages are measured from conductor wrt common ground ?
Great Article. I was going crazy about the sprt(3) missing there, but when you talked of S-3phase and S-1phase it all made sense.
Thank you very much for taking the time to explain in this length and detail; great work!