![]()
While not an individual exam topic, complex numbers and vector mathematics are a key fundamental skill that appears on numerous questions throughout the exam.
You can expect to see them anytime complex impedances, apparent power, and phasors with a magnitude and angle appear.
It helps to have a comfortable understanding of what complex numbers are and how to use them.
First, some definitions:
(You may skip these and jump down to where the action is at if this is not new for you)
Vector – A quantity that has two values, magnitude (size), and direction (angle).
Phasor – An electrical quantity represented as a vector, that equates to a sine wave value.
Remember that even though we are most familiar working with the RMS value of voltage like 110 to 120 volts in our house, and 277 to 480 volts in commercial buildings, alternating voltage is actually a varying sine wave.
A Phasor is a simple way of using a vector to represent a sinusoidal function using a magnitude and angle.
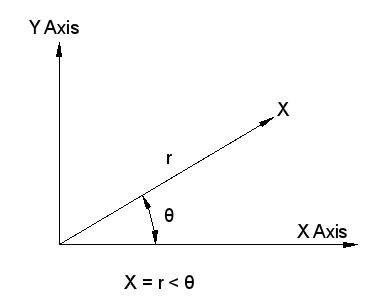
Polar – A way to represent a vector using a magnitude and an angle.
A polar vector takes on the form of V = |r|<θ, where |r| is the magnitude and θ is the angle in degrees.
Magnitude – The size and length of the vector.
If you’ve ever drawn a “power triangle” to show the apparent power in Volt Amps, or VA, then the hypotenuse of the triangle is the magnitude.
Magnitude takes on the form of absolutel value and can never be negative.
An example of a magnitude is: |r|
Phase angle – The angle of a vector in respect to the the right hand horizontal axis.
The most standard electrical Phase sequence is Positive ABC, which means that phasors rotate around the phasor diagram counter clockwise.
For ABC sequence any angle that is counter clock wise from the zero axis is positive, and any angle that is clock wise from the zero axis is negative.
The opposite is true for Negative ACB.
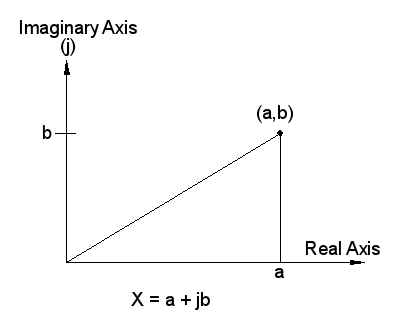
Complex Rectangular – A way to represent a vector using a real component and an imaginary component.
Back to the “power triangle” example the real component is the horizontal leg of the triangle and imaginary component is the vertical leg of the triangle.
A complex rectangular number takes on the form of V = a + jb.
Real Component – The horizontal component of a complex number.
If V = a + jb, the value of the real component is a.
The real component can also be expressed as Re{V} = a.
Imaginary Component – The vertical component of a complex number.
If V = a + jb, the value of the imaginary component is b.
The imaginary component can also be expressed as Img{V} = b.
Ignore the lower case j when a vector is represented in complex rectangular form, it is merely used to distinguish the imaginary component from the real component.
Conjugate – Marked by an asterisk *
When a conjugate is applied to a:
Complex number – the polarity of the imaginary component changes.
Polar number – the polarity of the angle changes.
Next, Graphing and Notation:
Complex or rectangular number “Z hat” with a real component R and imaginary component X:

Vector or polar number “S hat” with a magnitude |S| and angle “theta S”:

Video – Graphing Polar vs Complex
Converting Between Polar and Complex
Remember that a vector can be expressed in polar or complex form.
This means that we can convert back and forth between the forms.
If we start with a polar number:

we can solve for the real (a), and imaginary (b) components of the same vector expressed as a complex number by the following formulas:

We can now re-write the same vector as a complex number:

Now, moving backwards, if we want to express the complex number as a polar number, we can solve for the magnitude |r| and angle θ with the following formulas:
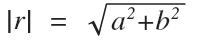

We can now re-write the complex number as a polar number:

Let’s see what it looks like done live with the following video:
Video – Converting Between Polar and Complex
Vector Math
So we just learned how to convert back and forth between the two forms.
But why the heck would we ever want to do that?
The simple answer, is to be able to carry out math properly with vectors.
Unless you have a more sophisticated calculator, the following is always true:
Addition & Subtraction can only be done with complex numbers
Multiplication & Division can only be done with polar numbers
This means if you need to add or subtract two vectors, and one is in polar form, you better make sure to convert it to a complex number first or you will get the wrong answer.
This also holds true if you need to multiply or divide two vectors, and one is in rectangular form, you will need to convert it to polar form first.
So now we know how and when to convert, let’s look at how to add, subtract, multply, and divide.
Addition
Add the real components together, and the imaginary components together.
The new complex number is the sum of the real components, and the sum of the imaginary components.
Order does not matter.
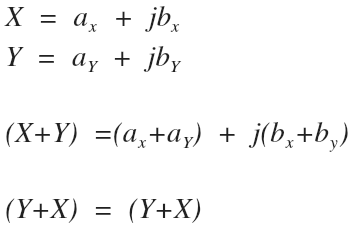
Subtraction
Subtract the real components, and the imaginary components.
The new complex number is the difference of the real components, and the difference of the imaginary components.
Order does matter.

Multiplication
Multiply the magnitudes and add the angles.
The new magnitude is the product of both magnitudes.
The new angle is the sum of both angles.
Order does not matter.
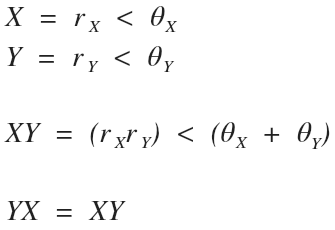
Division
Divide the magnitudes and subtract the angles.
The new magnitude is the quotient of both magnitudes.
The new angle is the difference of both angles.
Order does matter.
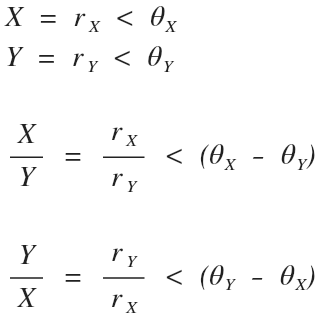
Now let’s see what vector math actually looks like live with a couple of examples by hand:
Video – Vector Addition, Subtraction, Multiplication, & Division Examples
That’s it!
Easy as pie, right?
Would you like to share?
Comment below and share your experience using complex numbers for the Electrical Power PE Exam.
Be sure not to give away any specific exam questions or answers per the NCEES policy.

I have never known such in depth of this until now, after 27 years. You are such a gifted teacher, Zach. Thank God that we found you. More power to you and your great mission!!!
Thanks, Holly, glad you found the information knowledge.
Complex Numbers, vectors, and phasors are things I don’t want to struggle with while taking the PE Exam. This article is great because it explains exactly what you need to know…Add and Subtract using Rectangular numbers, Multiply and Divide using Polar numbers. Great article!
I’m happy I was able to understand and grab this teaching.
I’m so grateful.
I can’t help but proofread as I go down the article. I swear it helps me study XD
In the definitions…
“Phasor – An electrical quantity represented as a vector, that equates to a sin wave value.
Remember that even though we are most familiar working with the RMS value of voltage like 110 to 120 volts in our house, and 277 to 480 volts in commercial buildings, alternating voltage is actually a varying sin wave.”
Since everything else is written out, spelling out “sine wave” with the “e” will help the sentence read easier, in the two instances where that appears.
“Magnitude takes on the form of absolutely value and can never be negative.”
Should say “absolute” here, not “absolutely”
“Phase angle” – bold face formatting error
Also clockwise and counterclockwise are both one word. You have them incorrectly broken out into separate words in the three instances where they appear.
Everything else looks good. Towards the end of the article under “Addition” you should capitalize “Add” in the first sentence.
Thanks for bringing these to my attention as well Josh!
Thank you! This is really helpful, but is polar and phaser solved the same way? I understand the difference where polar is a vector with magnitude and angle, while phasor is the same but becomes a sine wave, however how do I know which is which? In a circuit do I always assume it is phasor with an AC source? Is converting it to rectangular form different for a phasor vs polar? How do I differentiate the two?
Hi Jennifer,
Typically, when we use the word “phasor” we are referring to a complex number in electrical engineering expressed in either polar form with a magnitude |r| and angle (θ):
|r|<θ
Or, expressed in rectangular form with a real component (a) and an imaginary component (b):
a + jb
With electrical power engineering, these are always RMS values.
We can express phasors in the time domain using sine (or cosine) signals. Instead of an RMS magnitude, we have a peak (or “maximum”) value:
Vm = √2(Vrms)
Instead of an angle phase shift, we have a time phase shift in seconds.
For example, an AC RMS voltage with a magnitude of 120 volts and a zero-degree phase shift in polar form is:
V = 120V<0º
In the time domain, the function becomes:
v(t) = √2(120)·sin(wt)
where:
w = 2πf in units of radians per second.
When studying for the PE exam, we are typically only concerned with the time domain and sine or cosine signals when working with Power Electronics and Devices.
There is an entire module available in our free trial dedicated to this subject:
Free Trial – Power PE Review Course
Hey Zach; appreciate the building block approach here. question on the phasor definition: ‘An electrical quantity represented as a vector that equates to a sine wave value’. would we still call composite wave forms other than pure 1x sine waves( be that one with harmonics or something like saw tooth) phasors? If still called phasors for waveforms other than sine, would we still call largest amplitude of that waveform the phasor magnitude and the phase angle of that largest amplitude the phase or would we be decomposing into series and calling the 1x or largest component the phasor magnitude?
I think this is probably a mute point for quick calcs we do on an exam were we have handy averages like RMS or DC but wanted to square some of these terms / deffs with other applications that I use polar/rectangular descriptions in.
thanks!
thanks for the insight.